Funções Trigonométricas
As funções trigonométricas têm seu estudo iniciado no 2° grau, no entanto a falta de habilidade dos professores em transmitir a importância do entendimento destas funções gera um esquecimento generalizado além de uma grande confusão na cabeça dos estudantes, os quais apenas decoram alguns valores de funções trigonométricas para ângulos muito utilizados.
Vamos aqui tentar esclarecer a utilização das funções trigonométricas. Inicialmente temos que entender qual é o significado de graus e radianos.
Ambos definem a mesma coisa, porém o primeiro tem a unidade de grau e o segundo é apenas um número sendo utilizado em equações e cálculos.
Definimos que uma circunferência completa é subdividida em 360° ou então 2 rad.
Um dos principais problemas dos alunos está em entender o significado de , não é alguma função mágica difícil de ser entendida, é simplesmente um número irracional dado aproximadamente por 3,14. Temos então 6,28 rad aproximadamente em uma circunferência.
Aplicando a regra de três para graus e radianos obtemos que 1rad=180/(ou 1°=/180. Para definirmos as funções trigonométricas vamos utilizar uma circunferência de raio 1.
Por convenção, o ponto inicial desta circunferência se encontra na extremidade direita.
Se caminharmos uma quantidade positiva em graus ou radianos, devemos percorrer a circunferência no sentido anti-horário, e para quantidades negativas, devemos percorrê-la em sentido horário.
Posicionando esta circunferência de forma que seu centro coincida com o ponto central das coordenadas cartesianas, a função senx é definida como sendo a projeção no eixo y e a função cosx é definida como sendo a projeção no eixo x de um dado ponto localizado na circunferência.
Uma vez que estas funções estão definidas apenas dentro de uma circunferência de raio 1, o valor máximo que cada uma pode atingir é 1, além disto, depois de cada volta completa os valores de seno e cosseno começam a se repetir, dizemos portanto que as funções seno e cosseno são funções periódicas de período 2(pois sen=sen(+2) e cos=cos(+2)).
Podemos agora definir outras quatro funções trigonométricas através da definição de seno e cosseno: tan=sen/cos; cotan=cos/sen; sec=1/cos; cossec=1/sen.
Importante de ser lembrada é a relação fundamental trigonométrica: sen2+cos2=1.
Dividindo esta última relação por cos2(temos outra relação importante dada por tan2+1=sec2.
Temos ainda as fórmulas de adição para seno, cosseno e tangente, dadas respectivamente por sen(+)=sencos+cossen, cos(+)=coscos+sensen(e 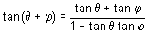 ).
).
As fórmulas de subtração são análogas, bastando para obtê-las inverter todos os sinais indicados nas equações acima.
Existem também as chamadas fórmulas do ângulo-duplo e fórmula do ângulo-metade, fórmulas as quais são deduzidas a partir da soma e subtração de ângulos, porém devido ao seu uso generalizado, é bom sabê-las de cor.
Temos então para o ângulo-duplo: 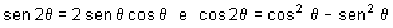 .
.
Para o ângulo-metade as fórmulas são: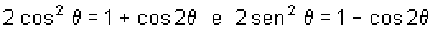 .
.
Já entrando em cálculo, temos que a derivada de seno é o cosseno da função, assim como a derivada de cosseno é igual a menos seno.
Para calcular estas derivadas, basta aplicarmos a definição de derivada e saber o valor dos limites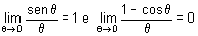 .
.
As derivadas de funções trigonométricas de funções são dadas pela fórmula de derivação de funções compostas da seguinte maneira: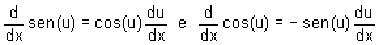 , onde u é uma função qualquer de x.
, onde u é uma função qualquer de x.
Podemos finalmente citar a existência das funções trigonométricas hiperbólicas, as quais aparecem ocasionalmente em determinadas aplicações.
O cosseno e o seno hiperbólicos são definidos da seguinte maneira: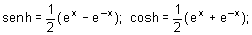 .
.
A partir destas definições, podemos também obter a tangente, a secante e a cossecante hiperbólicas.
A diferença básica entre as funções trigonométricas e as trigonométricas hiperbólicas é a não periodicidade das últimas.
Funções Trigonométricas Inversas
As funções trigonométricas inversas são as funções arc senx (lê-se arco seno de x), arc cosx e arc tanx.
Estas funções também são representadas por sen-1x=arc senx, cos-1x=arc cosx e tan-1x=arc tanx.
Temos que esclarecer também que a função sen-1x assim como cos-1x e tan-1x não são igual a 1/senx.
A utilidade inicial destas funções era a de permitir o cálculo das seguintes integrais: 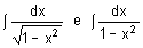 .
.
No cálculo da primeira integral por exemplo, o termo na parte inferior da integral é um tanto complicado, porém podemos fazer a substituição x=sen, e desta forma temos a raiz de 1-sen2.
Utilizando a relação fundamental da trigonometria temos sen2+cos2=1, portanto 1-sen2= cos2. Uma vez que x=sen, dx/d=cos, logo dx=cosd.
A equação que nos resta então é igual a 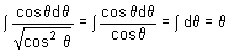 .
.
Surge aqui então que a solução da integral acima é um ângulo, e surge também a definição de arc sen.
Como a função arc sen é a função inversa de sen temos que arc sen(x)=y e sen(y)=x.
Fazendo substituições do mesmo tipo conseguimos chegar à resolução da segunda integral definindo então a função arc tan.
A definição para as funções trigonométricas inversas é definida como o ângulo cujo seno é x, ou ângulo cujo cosseno é x e assim em diante.
Os gráficos das funções trigonométricas inversas podem ser esboçados a partir dos gráficos das funções das quais elas são originadas, bastando para isto apenas inverter a posição dos eixos coordenados.
Veja também:







