Lei de Ampère

Numa região de campo magnético, consideremos uma linha fechada C dividida em um grande número N de segmentos (elementos de comprimento) Dlk (k = 1, 2, … N), pequenos o suficiente para que, sobre cada um deles, o campo possa ser considerado constante.

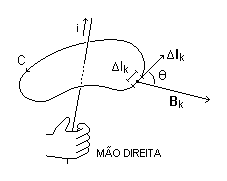
A cada elemento de comprimento Dlk associamos um vetor Dlk.

A grandeza:
c = S Bk.Dlk = S Bk Dlk cos q

onde o somatório sobre k se estende de 1 a N, é chamada circulação do campo magnético ao longo da linha C.

A lei de Ampère afirma que a circulação do campo magnético ao longo de uma linha fechada que envolve as correntes i1, i2, … iM é:

S Bk.Dlk = moi[Linha Fechada]

onde i = i1 + i2 + … + iM.

Quando se aplica essa equação deve-se considerar a linha fechada, chamada de amperiana, e, portanto, todos os elementos Dl1, Dl2, … DlN, orientados segundo os dedos da mão direita com o polegar na direção da corrente total i.

Como exemplo do uso da lei de Ampère vamos calcular o campo magnético ao redor de um fio reto, de comprimento infinito, por onde passa uma corrente i.

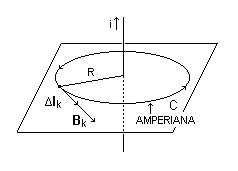
Pela simetria do problema, o módulo do campo magnético num ponto qualquer deve depender apenas da distância do ponto ao fio.

Assim, escolhemos para o cálculo da circulação uma circunferência de raio R, centrada no fio e num plano perpendicular ao fio.

Ainda pela simetria do problema temos que o campo em cada ponto da amperiana escolhida deve estar no plano da amperiana, numa direção perpendicular ou tangente a ela. Da experiência sabemos que o campo é, na verdade, tangente à amperiana.

Assim, como o ângulo entre Bk e Dlk é 0^O e como o campo magnético tem o mesmo módulo em todos os pontos da amperiana, segue-se que:

S Bk.Dlk = B S Dlk cos 0^O = B 2pR

e pela lei de Ampère:

B 2pR = moi
ou
B = moi / 2pR

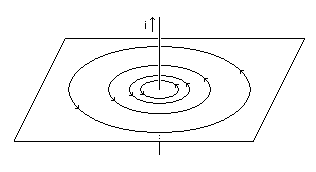
Assim, as linhas do campo magnético de um fio reto infinito são circunferências concêntricas, com centro no fio.

Fonte Texto:
http://www.ufsm.br/gef/Eletro08.htm

Fonte Imagem:
http://n.i.uol.com.br/licaodecasa/ensmedio/fisica/ampere-01.jpg