Cubo
É, de entre todos os poliedros, talvez o mais conhecido, dado existirem muitos objetos de uso corrente de forma cúbica, como por exemplo um dado.
O cubo é um poliedro regular pois as suas faces são geometricamente iguais.
O cubo tem os seguintes elementos:
* 6 faces, que são quadrados geometricamente iguais;
* 12 arestas iguais, que são segmentos de reta;
* 8 vértices, que são pontos.
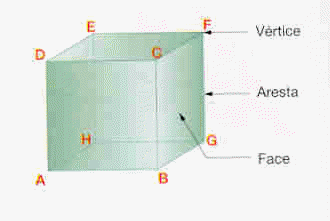
Para construir um cubo basta conhecer a medida de uma aresta.
Chama-se diagonal do cubo, D, ao segmento de reta que une dois vértices não pertencentes à mesma face.

A diagonal D do cubo é a hipotenusa do triângulo retângulo de catetos a e d: D2 = d2 + a2. Mas d é a hipotenusa do triângulo retângulo de catetos iguais a a, sendo a a medida da aresta do cubo, logo, d2 = a2 + a2, ou seja, d2 = 2a2. Então, D2 = 2a2 + a2 = 3a2, donde temos que o comprimento da diagonal do cubo é dada por D = 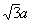 .
.
A área da superfície do cubo pode calcular-se facilmente atendendo ao fato das suas faces serem 6 quadrados iguais.

Sendo a o comprimento da aresta do cubo, a área de cada face será a2, e portanto, temos:
* Área lateral do cubo:
A área lateral do cubo é a soma das áreas das faces laterais, sendo dada por:
Al = 4a2 , onde: Al – área lateral
* Área total do cubo:
A área total do cubo é a soma da área lateral com a área das duas bases, ou seja:
At = Al + 2Ab= 4a2 + 2a2 = 6a2, onde: At – área total
Al = 4a2 – área lateral
Ab = a2 – área da base
O volume do cubo é dado pelo cubo (terceira potência) do comprimento da aresta.
Assim, sendo a o comprimento da aresta do cubo, o seu volume é V=a3.
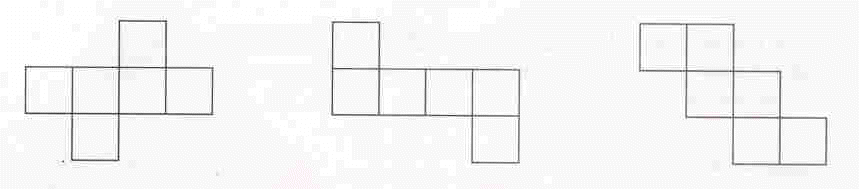
Algumas planificações: