Pirâmides

…É um poliedro em que uma das faces é um polígono qualquer, a que se chama base; as outras faces são triângulos que têm um vértice comum, chamado vértice da pirâmide.

Uma pirâmide diz-se reta, se o projeção do vértice da pirâmide coincide com o centro da base. Uma pirâmide reta cuja base é um polígono regular diz-se uma pirâmide regular. Nas pirâmides regulares, as faces laterais são triângulos isósceles. Quando a projeção do vértice não coincide com o centro do polígono da base, diz-se que a pirâmide é oblíqua.

Altura de uma pirâmide é a distância do vértice da pirâmide ao plano da base. À altura de cada uma das faces laterais chama-se apótema da pirâmide. É evidente que, sendo a base um polígono regular, este também tem um apótema, a que se chama apótema da base.

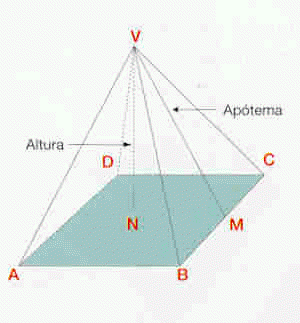
Numa pirâmide podemos encontrar os seguintes elementos:
* base (polígono);
* faces (triângulos);
* arestas da base (lados da base);
* arestas laterais (lados das faces que não pertencem à base);
* vértices da base (vértices do polígono da base);
* vértice da pirâmide (ponto de encontro das arestas laterais).

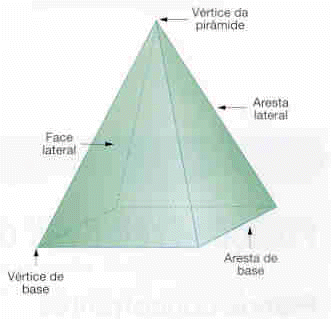
Tal como acontece com os prismas, também as pirâmides se classificam de acordo com o polígono da base.

Assim, teremos:
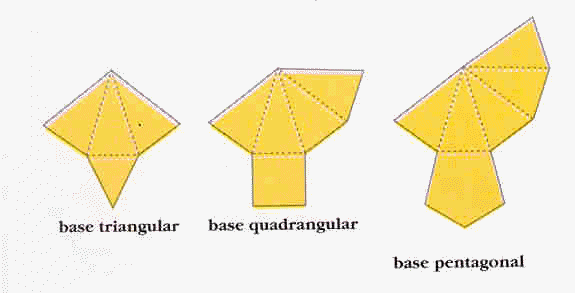
* pirâmide triangular (três faces; base é um triângulo);
* pirâmide quadrangular (quatro faces);
* pirâmide pentagonal (cinco faces);
* pirâmide hexagonal (seis faces);
* etc.

Quando a pirâmide é formada por quatro triângulos equiláteros geometricamente iguais, tem o nome especial de tetraedro, que é um poliedro regular porque as suas faces são polígonos regulares sobreponíveis e é idêntico em todas as faces, isto é, neste poliedro não há vértices nem bases especiais. Em geral, uma pirâmide regular não é um poliedro regular.

Para que os alunos compreendam o processo pelo qual se determina a área da superfície de uma pirâmide regular, sugerimos a construção de uma pirâmide quadrangular em cartolina, cuja base tenha 49 cm² de área e cujo apótema tenha 10 cm.

Atendendo à planificação, os alunos poderão ver facilmente que a área não é mais do que a soma da área lateral, A_l (sombreada a vermelho), com a área da base, A_b (sombreada a cinzento):

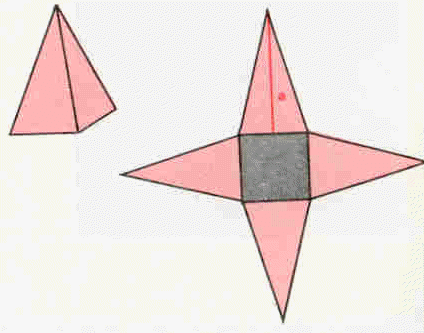
A área lateral é a soma das áreas das faces (triângulos isósceles). Sendo p o perímetro da base, A_l = (p × a) ÷ 2 . A área total será, então, dada pela seguinte fórmula: A_t = (p × a) ÷ 2 + A_b .

Para entender a fórmula que permite calcular o volume de uma pirâmide, podemos pensar num caso muito evidente: uma pirâmide quadrangular regular cuja base seja uma face de um cubo (de aresta a) e cujo vértice seja o centro desse cubo.

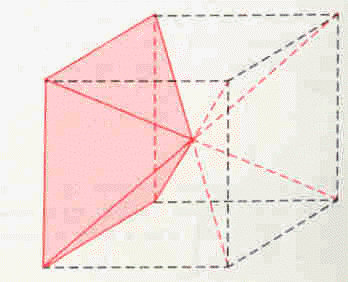
Vê-se claramente que no cubo cabem seis pirâmides iguais àquela – tantas quantas as faces do cubo. O volume de cada uma é, então, a sexta parte do volume do cubo, ou seja, V = a³ ÷ 6. Como a altura, h, de cada pirâmide é metade da aresta do cubo, ou seja, a aresta do cubo vale 2h, temos então que o volume da pirâmide pode ser escrito da seguinte forma: V = (A_b × 2h) ÷ 6 = (A_b × h) ÷ 3 , e portanto, o volume de uma pirâmide é igual a um terço do produto da área da base pela sua altura.

O Princípio de Cavalieri autoriza-nos a afirmar que esta conclusão é válida para qualquer pirâmide.

Planificações:

Fonte:
http://www.educ.fc.ul.pt/icm/icm99/icm21/piramides.htm