Triângulos Semelhantes
Podemos identificar na figura ao lado dois triângulos: um limitado pela reta amarela , que chamaremos de ABD, pois esses três pontos definem o triângulo; e outro maior que podemos chamar , pela mesma razão do primeiro, AFE. Se você mover os pontos A,B ou D verá que eles mantém as mesmas características entre si: mesmo formato e proporção entre os tamanhos: neste caso cada lado do maior tem o dobro do tamanho do menor.
Triângulos podem ser semelhantes em três casos, se e somente se:
LAL(lado, ângulo, lado) – possuem dois lados proporcionais – como na figura onde AE é duas vezes maior que AD e AF é duas vezes maior que AB : med(AE)=2*med(AD), med (AF)=2*med(AD). E esses lados devem formar um ângulo congruente – na figura , como os triângulos estão “um sobre o outro” o ângulo em A é o mesmo para os dois.
AA(ângulo, ângulo) – possuem dois ângulos congruentes;
LLL(lado, lado, lado) – possuem os três lados proporcionais.
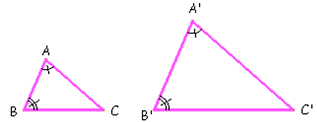
Fonte: Mathematikos.psico.ufrgs.br



