Determinantes

Determinante de uma matriz quadrada
Se A é uma matriz quadrada A de ordem 2, dada por:

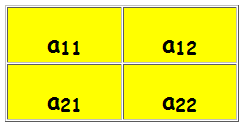
definimos o determinante desta matriz A, denotado por det(A), como:

det(A) = a11.a22 – a21.a12

Se A é uma matriz quadrada A de ordem 3, dada por:

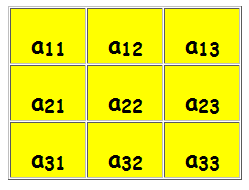
definimos o determinante desta matriz A, como:

det(A) = a11.a22.a33 + a21.a32.a13 + a31.a12.a23
– a11.a32.a233 – a21.a12.a33 – a31.a22.a13

Propriedades dos determinantes
Seja A uma matriz quadrada de ordem n maior ou igual a 2.
1. Se uma linha (ou coluna) da matriz A for nula, então: det(A)=0

2. O determinante da transposta de A é igual ao determinante de A, isto é: det(At)= det(A)

3. Se B é a matriz obtida pela multiplicação de uma linha (ou coluna) da matriz A por um escalar k, então: det(B) = k det(A)

4. Se B é a matriz obtida pela troca de duas linhas (ou colunas) de A, então: det(B) = – det(A)

5. Se A tem duas linhas (ou colunas) iguais, então: det(A) = 0

6. Se uma linha ( ou coluna) de A for múltipla de uma outra linha (ou coluna) de A, então: det(A) = 0

Fonte:
http://br.geocities.com/escolaaggeo/determinantes.htm