Sistemas Lineares
Introdução
Esta página trata sobre equações lineares e tem início mostrando uma aplicação de matrizes e sistemas lineares. As equações lineares assim como os sistemas de equações são muito utilizados no cotidiano das pessoas.
Exemplo: Uma companhia de navegação tem três tipos de recipientes A, B e C, que carrega cargas em containers de três tipos I, II e III. As capacidades dos recipientes são dadas pela matriz:

Quais são os números de recipientes x1, x2 e x3 de cada categoria A, B e C, se a companhia deve transportar 42 containers do tipo I, 27 do tipo II e 33 do tipo III.
Montagem do sistema linear:
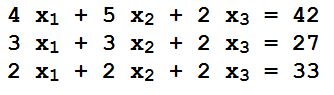
Equação Linear
É uma equação da forma
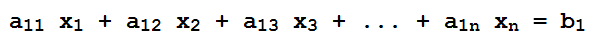
onde:
– x1, x2, …, xn são as incógnitas
– a11, a12, …,a1n são os coeficientes ( números reais ou complexos)
– b1 é o termo independente ( número real ou complexo)
Exemplos de equações lineares
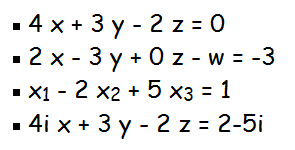
Exemplos de equações não–lineares
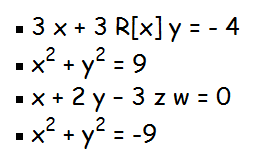
Observação: R[x] é a raiz quadrada do número real x não negativo.
Solução de uma Equação Linear
Uma sequência de números reais (r1, r2, r3, r4) é solução da equação linear
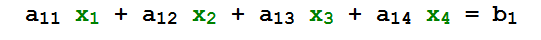
se
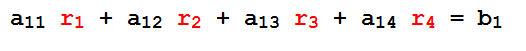
o que significa que se trocarmos cada xi por ri a equação deverá ser identicamente satisfeita.
Exemplo: A sequência (2,1,3) é uma solução da equação 2x+y–2z=-1 pois, trocando-se x por 2, y por 1 e z por 3 na equação dada, teremos:
2.(2) + 1.(1) –2.(3) = -1
Sistemas de Equações Lineares
Um sistema de equações lineares ou sistema linear é um conjunto composto por duas ou mais equações lineares. Um sistema linear pode ser representado da seguinte forma:
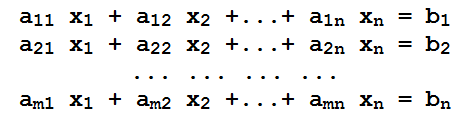
onde:
– x1, x2, …, xn são as incógnitas
– a11, a12, …, amn são os coeficientes
– b1, b2, …, bm são os termos independentes
Solução de um sistema de equações lineares
Uma sequência (r1, r2, …,rn) é solução do sistema
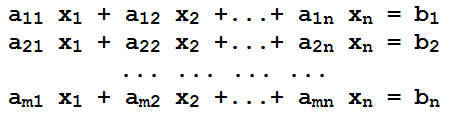
se satisfAz identicamente a todas as equações desse sistema.
Exemplo: A sequência (2,0) é uma solução do sistema linear:
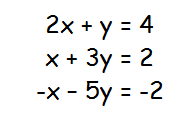
pois satisfaz identicamente todas as equações do mesmo, isto é, se substituirmos x por 2 e y por 0, os dois membros de cada igualdade serão iguais em todas as equações.
Classificação de Sistemas Lineares
O número de soluções de um sistema linear determina a sua classificação de duas maneiras com relação à sua consistência: sistema possível (consistente) ou sistema impossível (inconsistente).
Sistema possível ou consistente
Quando tem pelo menos uma solução.
Sistema impossível ou inconsistente
Quando não admite qualquer solução.
Exemplo de um sistema com uma única solução
As equações lineares representam retas no plano cartesiano que tem um ponto como interseção.
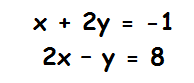
Solução = {(3,-2)}
Exemplo de um sistema com infinitas soluções
As equações lineares representam retas paralelas e sobrepostas no plano cartesiano, logo existem infinitos pontos que satisfAzem a ambas as equações.
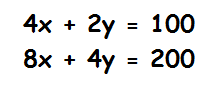
Exemplo de um sistema que não tem solução
As equações lineares representam retas paralelas no plano cartesiano, logo não existem pontos que pertençam às duas equações.
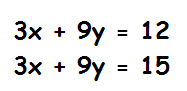
Sistemas Equivalentes
Dois sistemas são equivalentes se admitem a mesma solução.
Exemplo: Os sistemas
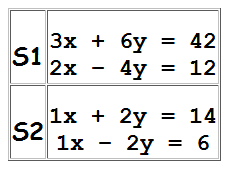
são equivalentes pois admitem a mesma solução x=10 e y=2.
Notação: Quando dois sistemas S1 e S2 são equivalentes, usamos a notação S1~S2.
Operações elementares sobre sistemas lineares
Existem três tipos de operações elementares que podem ser realizadas sobre um sistema linear de equações de forma a transformá-lo em um outro sistema equivalente mais simples que o anterior. Na sequência trabalharemos com um exemplo para mostrar como funcionam essas operações elementares sobre linhas. O segundo sistema (o que aparece à direita) já mostra o resultado da ação da operação elementar. Nas linhas iniciais de cada tabela, você encontra a operação que foi realizada.
– Troca de posição de duas equações do sistema

– Multiplicação de uma equação por um número real não nulo

– Adição de duas equações do sistema

Resolução de Sistemas Lineares por Escalonamento
Com o auxílio das três Operações Elementares sobre linhas, podemos resolver sistemas lineares. Vamos mostrar como funciona este processo através de um exemplo.
Exemplo: Consideremos o sistema com 3 equações e 3 incógnitas.
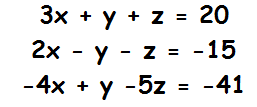
Observação: Indicaremos por Li + Lj -> Lj para significar que somamos a linha i com a linha j e colocamos o resultado na linha j e indicaremos k * Li -> Li, para significar que multiplicamos a linha i pela constante k e colocamos o resultado na linha i.




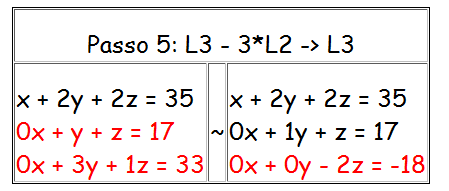


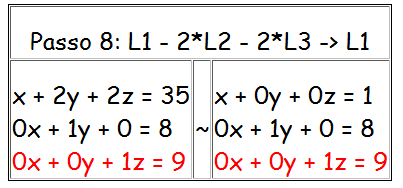
Após a operação de escalonamento, observamos que o último sistema pode ser reescrito como:
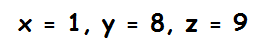
que é um sistema simples que fornece a solução do sistema.
Sistemas Lineares Homogêneos
Um sistema linear é homogêneo quando os termos independentes de todas as equações são nulos. Todo sistema linear homogêneo admite pelo menos a solução trivial, que é a solução identicamente nula. Assim, todo sistema linear homogêneo é possível. Este tipo de sistema poderá ser determinado se admitir somente a solução trivial ou indeterminado se admitir outras soluções além da trivial.
Exemplo: O sistema

é determinado, pois possui a solução
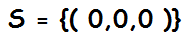
Regra de Cramer
Esta regra depende basicamente sobre o uso de determinantes. Para indicar o determinante de uma matriz X, escreveremos det(X). Seja um sistema linear com n equações e n incógnitas:
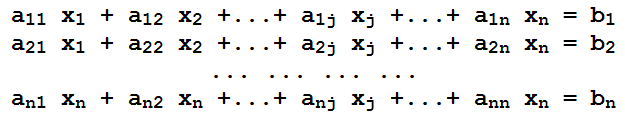
A este sistema podemos associar algumas matrizes:
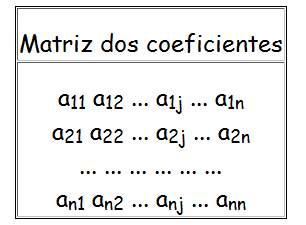
Matriz dos coeficientes
Formada pelos coeficientes das incógnitas do sistema. Comumente indicada pela letra A.
Matriz Aumentada do sistema
Formada todos os coeficientes das incógnitas do sistema e também pelos termos independentes.

Matriz da incógnita xj
É a matriz Aj obtida pela substituição da coluna j (j=1,…,n) da matriz A, pelos termos independentes das equações do sistema.
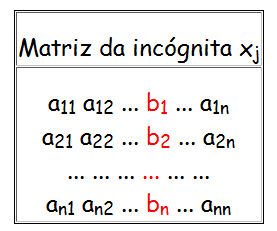
Quando as posições j=1,2,3 estão relacionadas com x1, x2 e x3 e substituídas pelas incógnitas x, y e z, é comum escrever Ax, Ay e Az.
Se det(A) é não nulo, é possível obter cada solução xj (j=1,…,n), dividindo det(Aj) por det(A), ou seja;
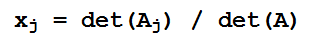
Se det(A) = 0, o sistema ainda poderá ser consistente, se todos os determinantes nxn da matriz aumentada do sistema forem iguais a zero.
Exemplo: Tomemos o sistema
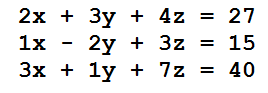
A matriz A e a matriz aumentada A~ do sistema estão na tabela, em anexo. Como det(A)=0, há a necessidade de verificar se todos os determinantes de matrizes com 3 linhas e 3 colunas da matriz aumentada são nulos.
Se existir pelo menos um deles não nulo, o sistema será impossível e este é o caso pois é não nulo o determinante da sub-matriz 3×3 formada pelas colunas 1, 2 e 4 da matriz aumentada:
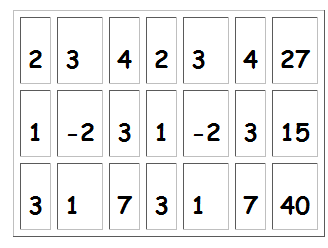
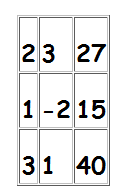
Conclusão: Este sistema é impossível.
Exemplo: Consideremos agora o sistema (Quase igual ao anterior: troquei 40 por 42 na última linha!)
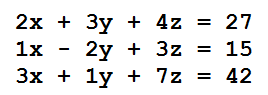
A matriz A e a matriz aumentada A~ do sistema, aparecem na tabela:

Aqui, tanto det(A)=0 como todos os determinantes de matrizes com 3 linhas e 3 colunas da matriz aumentada são nulos, então o sistema é possível e indeterminado.
Neste caso pode-se observar que a última linha é a soma das duas primeiras e como estas duas primeiras dependem de x, y e z, você poderá encontrar as soluções, por exemplo, de x e y em função de z.
Exemplo: Seja o sistema
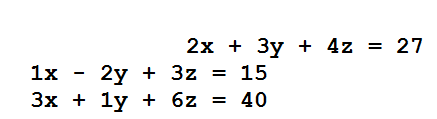

As matrizes A e a dos termos independentes do sistema estão na tabela, em anexo. Como det(A)=7, o sistema admite uma única solução que depende dos determinantes das matrizes Ax, Ay e Az.
A matriz Ax é obtida pela substituição 1a. coluna da matriz A pelos termos independentes das três equações e ela é dada por:
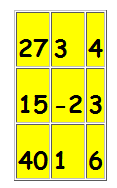
e det(Ax)=65.
A matriz Ay é obtida pela substituição da 2a. coluna da matriz A pelos termos independentes das três equações e ela é dada por:

e det(Ay)=1.
A matriz Az é obtida pela substituição da 3a. coluna da matriz A pelos termos independentes das três equações e ela é dada por:
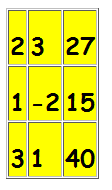
e det(Az)=14.
Podemos agora obter a solução do sistema dada:
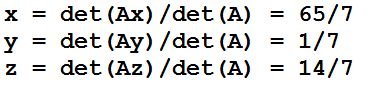
Fonte:
http://br.geocities.com/escolaaggeo/lineares.htm

