Pêndulo de Foucault
Saiba o verdadeiro significado do Pêndulo de Foucault
O famoso Pêndulo de Foucault, nomeado em homenagem ao seu inventor físico francês Jean Benard León Foucault, é parte de um experimento científico com o objetivo de mostrar a terra em rotação, sem observações astronômicas, simplesmente usando a inércia do movimento de nosso planeta e um pêndulo.
Foucault instalou uma esfera de cobre de 30 kg suspensa a alguns centímetros do chão, envolvido por um cabo de aço de 67 metros fixado no teto da cúpula do Panteão de Paris, certificando-se que nada pudesse interferir ou condicionar seu movimento. O pingente foi equipado com uma ponta de metal na parte inferior para fazer uma carreira de areia.
No experimento, o pêndulo ficou em movimento e depois de uma hora, Foucault pode notar alterações em sua trajetória, a qual foi mudada em vários graus na direção dos ponteiros do relógio devido ao efeito de Coriolis (aceleração angular), descrito por Gaspard-Gustave de Coriolis, durante o século XIX. O pêndulo varia seu caminho a cada 24 horas, mas esse movimento vai ser mais visível nos polos da terra.

A Força de Coriolis não e uma força em si mesma, mas a influência do movimento de um objeto que roda (terra neste caso) sobre objetos em movimento sobre a superfície, que empurram as massas para a curva no sentido horário no hemisfério norte e no sentido anti-horário no hemisfério sul.
Mais informações
Uma consequência da rotação da Terra é a rotação noturna de estrelas através do céu. Todavia, olhando para as estrelas, não podemos dizer se é a Terra que gira e as estrelas permanecem fixas, ou se a Terra é fixa e as estrelas descrevem círculos em torno dela. Por meio de um dispositivo chamado pêndulo de Foucault, obtemos evidência convincente de que é a Terra que gira. Ele demonstra que o fato de que a Terra não é um sistema de referência inercial.
A experiência realizada por Foucault foi em 1851, realizada na grande cúpula do Pantheon em Paris, usando um massa de 28 kg numa suspensão de fio de quase 70 m. A maneira pela qual a extremidade superior do fio era presa e permitia ao pêndulo oscilar livremente em qualquer direção. O período de um pêndulo deste comprimento é aproximadamente 17 segundos.
Em torno do ponto no solo, diretamente abaixo do ponto de suspensão, foi construída uma pequena elevação circular, de aproximadamente 3 metros de raio. Nesta elevação foi colocado um pouco de areia de modo que uma ponta metálica que saía do pêndulo (para baixo), varria a areia em cada oscilação.
Após sucessivas oscilações, tornou-se claro que o plano do movimento do pêndulo movia-se no sentido dos ponteiros do relógio, quando visto de cima. Numa hora, o pêndulo mudou seu plano de oscilação de mais de 11 graus. Uma volta completa foi concluída em aproximadamente 32 horas. Em cada oscilação o plano movia-se 3 mm, medidos no círculo de areia.
Por que gira o plano do pêndulo? Se a experiência de Foucault fosse realizada no Polo Norte, poderíamos ver, imediatamente, que o plano de movimento do pêndulo permaneceria fixo num sistema inercial, enquanto a terra gira sob o pêndulo, de uma volta completa cada 24 horas. A rotação da Terra é no sentido contrário ao dos ponteiros do relógio, quando vista de acima do Polo Norte, de modo que para um observador numa escada, sobre a terra, no Polo Norte, o plano do pêndulo parecia girar na direção horária.
A situação é diferente, quando deixamos o Polo Norte, e o tempo para uma volta completa é mais longo.
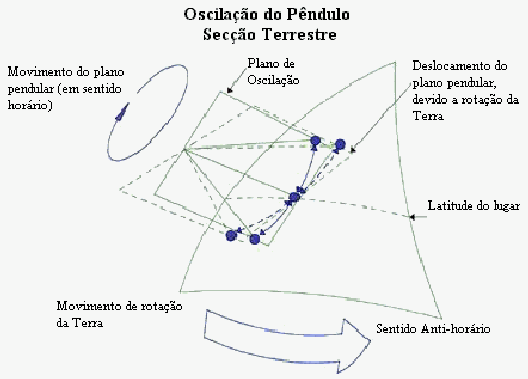
Considere as velocidades relativas dos pontos que são o extremo norte e sul do círculo de areia de raio r. O ponto sul é mais afastado do eixo de rotação da terra e portanto se moverá no espaço mais rapidamente que o ponto norte. Se w é a velocidade angular da terra e R o seu raio, então o centro do círculo de areia se move com velocidade wRcosq, onde q é a latitude de Paris (48o51’N), medido do equador da Terra. O ponto mais ao note do círculo de areia se move com velocidade
Vn = wR cosq – wr senq
como vemos na figura, e o ponto mais ao sul se move com velocidade
Vs = wR cosq + wr senq
A diferença entre cada uma destas velocidades e a do centro do círculo é
Dv = wrsenq
Se o pêndulo é posto a oscilar no plano norte-sul, por meio de um empurrão, a partir do repouso, no centro do círculo, a componente leste-oeste da velocidade no espaço será a mesma que a do centro do anel.
A circunferência do círculo é 2pr, de modo que o tempo T0 para uma volta completa é, se Dv for constante em torno do círculo,
T0 = 2pr / Wrsenq = (24 horas) / senq
No equador senq = 0 e o tempo se torna infinito.






