Lei de Gauss
Definição
Lei de Gauss (eletricidade)
A lei de Gauss relaciona o fluxo elétrico através de uma superfície fechada com a carga elétrica no interior da mesma. Assim, podemos enunciá-la como: “O fluxo elétrico total através de qualquer superfície fechada é proporcional à soma das cargas no interior desta superfície”.
Esta lei mostra uma relação muito importante entre a carga contida num elemento de volume e o fluxo de campo elétrico através da superfície que delimita o volume. Com isto podemos mostrar que as cargas positivas são fontes de campos divergentes e as negativas de campos convergentes.
Esta lei assegura a existência de monopolos elétricos, ou a existência de cargas elétricas isoladas e tem uma grande importância no cálculo de campos elétricos em sistemas cuja a distribuição de carga têm alta simetria. A equação, para a lei de Gauss, é válida sem restrições, mas em geral não é simples resolve-la.
Lei de Gauss (magnetismo)
A lei de Gauss para o magnetismo é definida de forma análoga à sua correspondente para a eletrostática. A diferença básica está no fato de
não existir monopolosmagnéticos. Isto implica que a integral do fluxo magnético, em um superfície fechada, será sempre igual a zero.
Deve-se notar, a propósito, que existem pesquisadores buscando a descoberta dos monopolosmagnéticos, pois não há razão concreta para que eles não existam. Caso isto se concretize será necessário adicionar um termo no lado direito da segunda equação.
Numa região de campo magnético, consideremos uma superfície S dividida em um grande número N de partes (elementos de superfície) DAk (k = 1, 2, … N), pequenas o suficiente para que, sobre cada uma delas, o campo possa ser considerado constante.
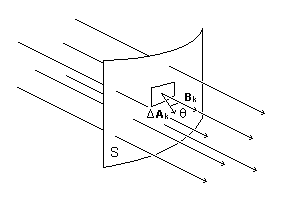
A cada elemento de superfície DAk associamos um vetor DAk, perpendicular ao correspondente elemento de superfície.
A grandeza:
f = S BkDAk
ou
f = S Bk DAk cos q
onde o somatório sobre k se estende de 1 a N, é chamada fluxo do campo magnético através da superfície S.
A lei de Gauss para o magnetismo expressa a inseparabilidade dos pólos magnéticos, ou seja, a inexistência de pólos magnéticos isolados (monopólos magnéticos).
Em termos do fluxo magnético, a lei de Gauss afirma: o fluxo do campo magnético através de qualquer superfície fechada é sempre nulo.
Matematicamente:
S BkDAk = 0 [Superfície Fechada]
Isto significa que toda linha de campo é uma linha contínua e fechada, ou seja, partindo do polo N vai ao polo S por fora do imã e, daí, por dentro, retorna ao polo N.
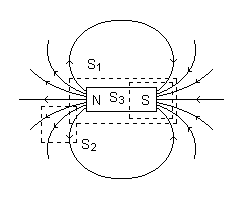
Portanto, é claro que o número de linhas de campo magnético que passam através de qualquer uma das três superfícies S1, S2 e S3 de fora para dentro é igual ao número de linhas de campo que passam de dentro para fora, de modo que o fluxo magnético total, para cada superfície, é nulo.
O mesmo vale para qualquer outra superfície fechada que se tome.







